INQUIRY ACTIVITY SUMMARY
Describe the 30* triangle
Click HERE.
Describe the 45* triangle
Click HERE.
Describe the 60* triangle
Click HERE.
1. The coolest thing I learned from this activity was...
how to find these points and coordinates mathematically instead of memorizing it by heart.
2. This activity will help me in this unit because...
I can now better understand how to label my triangles and my unit circle. It also showed me patterns I didn't notice before.
3. Something I never realized before about special right triangles and the unit circle is…
that they actually relate to each other! I was told that in past math courses, but I didn't quite grasp what it meant.
Saturday, February 22, 2014
Monday, February 10, 2014
RWA#1: Unit M Concept 5: Graphing Ellipses Given an Equation and Identifying All Parts
1. The mathematical definition of an ellipse is "the set of all points such that the sum of the distance from two points is a constant." (http://www.mhhe.com/math/precalc/barnettca2/student/olc/graphics/barnett01caaga_s/ch07/downloads/pc/ch07section2.pdf)
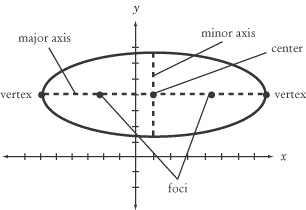
2. An ellipse is algebraically shown with the equation written in standard form: (x-h)^2/a^2+(y-k)^2/b^2=1 or (x-h)^2/b^2+(y-k)^2/a^2. The center is always (h,k). "a" is always bigger than "b." Remember that a and b are squared in the equation, so you have to take the square root of them when writing them out on the template.
It can be graphically shown as a visual on a graph. An ellipse typically looks like a squished circle from its sides or top and bottom.
Here is how you can identify key parts on the graph:
If a is under x in the equation (the first one listed above), the graph will be fat. The major axis length is 2a (Mrs. Kirch shows this with a solid line); the minor axis length is 2b (she shows this with a dotted line). In this kind of equation, the major axis will run horizontally.
To find vertices: Count "a" units from the center going left and right; plot these points. To find co-vertices: Count "b" units from the center going up and down; plot these points.
If a is under y in the equation (the second one listed above), the graph will be skinny. The major axis length is 2a; the minor axis length is 2b. In this kind of equation, the major axis will run vertically. To find vertices: Count "a" units from the center going up and down; plot these points. To find co-vertices: Count "b" units from the center going left and right; plot these points.
The foci effects the shape because the further away it is to the vertices, the more it will have to "focus" on that point. When the foci increases, the eccentricity does, too. To find your foci, the major axis value will be the number that does NOT change in the foci points. (ex. If the major axis is y=-2, your two foci will be (#, -2).) To find the other number, (ex. It would be x.), you take the value from your minor axis and add AND subtract it to/from your c value. In order to find c, you use the equation a^2+b^2=c^2.
Your eccentricity is greater than 0 but less than 1 and can be found with "c/a.
Do you want to see a problem worked out? Watch this video example.
3. A real world application of an ellipse would be when you tilt your glass cup with a drink to take a sip out of it. The drink in your cup will form an ellipse around the cup's interior. Let's take for example a glass of milk. When the milk is in the cup and set on the table, you may notice the top of the milk is shaped as a circle. Once you begin to tilt the cup and bring it to your mouth for a sip, the shape at the top of the milk is no longer a circle.

The ellipse is formed because the eccentricity has increased. It will continue to increase as you tilt the cup. The center of the ellipse moves further from the center of the cup the more you title your cup. I would associate this example as a skinny ellipse represented with the equation (x-h)^2/b^2+(y-k)^2/a^2 because the cup's ellipse would be facing me. The point closest to my lip and furthest to me would be the vertices. The left and right side of the cup would be my co-vertices.
4. Works Cited
Ellipse Image pasted from: http://img.sparknotes.com/content/testprep/bookimgs/sat2/math2c/0006/ellipse.gif
Tilted Milk Cup Image pasted from: http://lisamasson.photoshelter.com/image/I0000RM3hrmrL0Po
Ellipse Video Example video from: http://www.youtube.com/watch?v=wTGA9D4Y0qk
2. An ellipse is algebraically shown with the equation written in standard form: (x-h)^2/a^2+(y-k)^2/b^2=1 or (x-h)^2/b^2+(y-k)^2/a^2. The center is always (h,k). "a" is always bigger than "b." Remember that a and b are squared in the equation, so you have to take the square root of them when writing them out on the template.
It can be graphically shown as a visual on a graph. An ellipse typically looks like a squished circle from its sides or top and bottom.
Here is how you can identify key parts on the graph:
If a is under x in the equation (the first one listed above), the graph will be fat. The major axis length is 2a (Mrs. Kirch shows this with a solid line); the minor axis length is 2b (she shows this with a dotted line). In this kind of equation, the major axis will run horizontally.
To find vertices: Count "a" units from the center going left and right; plot these points. To find co-vertices: Count "b" units from the center going up and down; plot these points.
If a is under y in the equation (the second one listed above), the graph will be skinny. The major axis length is 2a; the minor axis length is 2b. In this kind of equation, the major axis will run vertically. To find vertices: Count "a" units from the center going up and down; plot these points. To find co-vertices: Count "b" units from the center going left and right; plot these points.
The foci effects the shape because the further away it is to the vertices, the more it will have to "focus" on that point. When the foci increases, the eccentricity does, too. To find your foci, the major axis value will be the number that does NOT change in the foci points. (ex. If the major axis is y=-2, your two foci will be (#, -2).) To find the other number, (ex. It would be x.), you take the value from your minor axis and add AND subtract it to/from your c value. In order to find c, you use the equation a^2+b^2=c^2.
Your eccentricity is greater than 0 but less than 1 and can be found with "c/a.
Do you want to see a problem worked out? Watch this video example.
3. A real world application of an ellipse would be when you tilt your glass cup with a drink to take a sip out of it. The drink in your cup will form an ellipse around the cup's interior. Let's take for example a glass of milk. When the milk is in the cup and set on the table, you may notice the top of the milk is shaped as a circle. Once you begin to tilt the cup and bring it to your mouth for a sip, the shape at the top of the milk is no longer a circle.

The ellipse is formed because the eccentricity has increased. It will continue to increase as you tilt the cup. The center of the ellipse moves further from the center of the cup the more you title your cup. I would associate this example as a skinny ellipse represented with the equation (x-h)^2/b^2+(y-k)^2/a^2 because the cup's ellipse would be facing me. The point closest to my lip and furthest to me would be the vertices. The left and right side of the cup would be my co-vertices.
4. Works Cited
Ellipse Image pasted from: http://img.sparknotes.com/content/testprep/bookimgs/sat2/math2c/0006/ellipse.gif
Tilted Milk Cup Image pasted from: http://lisamasson.photoshelter.com/image/I0000RM3hrmrL0Po
Ellipse Video Example video from: http://www.youtube.com/watch?v=wTGA9D4Y0qk
Ellipse website link pasted from: http://www.mhhe.com/math/precalc/barnettca2/student/olc/graphics/barnett01caaga_s/ch07/downloads/pc/ch07section2.pdf
Subscribe to:
Comments (Atom)