SP#7: Unit K Concept 10

This goes over how to write a repeating decimal as a rational number using geometric series. Make sure to use the infinite geometric series. The answer must be written as a fraction.

BQ #7 - Unit V

1. Where does the difference quotient come from?

-First you need to know that the difference quotient is known as finding the slope of the tangent line to a graph. On this graph, f(x), we're given a point on the line, which will be (x, f(x)). If we move to a different point, then that will be delta x, or h, for that matter. The new placing of the point, is the total value of x plus h. So at this new point, the values will be (x+h, f(x+h)), which, if you connect to the value (x, f(x)), will create a secant line. Given these points, we can find the slope of the secant line using the formula (y^2-y^1)/(x^2-x^1). We then insert the numbers that correspond with the formula, which will look like this: f(x+h)-f(x)/ x+h-x. If you then simplify, you get the difference quotient: f(x+h)-f(x)/b. Through the process of finding the slope of a secant line, we also find the slope of the tangent line, or the difference quotient.



Source:
1. http://cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG

BQ#6 – Unit U Concepts 1-8

1. What is continuity?
Continuity is a way to describe a function that is predictable.  It has no breaks, jumps, or holes.  This kind of function can be drawn on a graph without lifting your pencil. In addition, the value is the same as the limit.

What is discontinuity?
Discontinuity is a way to describe a function that is not predictable. There are two families: removable and non-removable discontinuities.
A point discontinuity is a removable discontinuity. Here the limit exists wherever the open circle is. This looks like a hole on the graph. Sometimes the value and the limit might not be at the same point. In this case, it is as if you and your friend plan to go to the mall and show up there, but it burned down.
In a non-removable discontinuity, the limit does not exist (NOT "there is no limit"). This includes a jump discontinuity where the graph is different coming from left and right. In this case, it is as if you and your friend plan to meet at a restaurant, but you two show up at different ones.  Oscillating behavior has no limit and the value is undefined because it is simply oscillating and appears wiggly on a graph.  In an infinite discontinuity (unbounded behavior) has vertical asymptote. This means it increases or decreases without bound toward infinity or negative infinity.

2. What is a limit?
A limit is the intended height of a function. We read a limit as: "The limit as x approaches 'a number' of f(x) is equal to 'L.'" You can have an infinite amount of limits on a graph.

 When does a limit exist?
The limit exists in continuous functions. This is when the intended is the actual height also. However, we must understand that the function is not the value. The three times a limit does not exist are when we have non-removable discontinuities. When it 'DNE,' we must also right the reasons. If it was a jump discontinuity, the graph is different left and right. If it was an infinite discontinuity, it has unbounded behavior. If it is oscillating, the graph is simply oscillating and we cannot find its value either which means it is undefined.

What is the difference between a limit and a value?
The limit is the intended height of the graph. Often this can be seen with two open circles or an open and closed circle. The value is the actual height. This is shown with a closed circle.

3. How do we evaluate limits numerically, graphically, and algebraically?
We can evaluate limits numerically which is on a table. The tables I have drawn in the pictures show how we can get really really really really close to a number without actually touching it.
Evaluating limits on a graph involves an actual graph. You put two fingers on the left and right side of where you want to evaluate a limit. If your fingers do not touch, the limit DNE.
Algebraically, you should first try the direct substitution method. We can get a number, 0 over a number which is 0, a number over 0 which means the limit DNE, or 0/0 which is the indeterminate form. If you get 0/0, use another method because it is "not yet determined" and we need to keep on working to find the answer. Whatever number the x approaches, you plug that into any variable of the equation given. You can also try the rationalizing/conjugate method.  Here you can use either the conjugate of the denominator or the numerator. You need to rearrange the equation given though by multiplying the top and bottom by the conjugate of either the numerator or denominator. Whichever conjugate you used, simplify it by FOILing. The non-conjugate will be left alone, so you can cancel things out. Remember, "...if something cancels, then your graph will have a HOLE!"

BQ#4 – Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” COtangent graph downhill? Use unit circle ratios to explain.
Tangent and cotangent are opposites of each other. Tangent=sin/cos. Whenever cos=0, tan is undefined because there would have to be asymptotes. The graph would go in a positive direction since they are positive in Quadrant 1 and Quadrant 3. Cotangent= cos/sin. Cotangent is positive in Quadrant 1 and Quadrant 3 as well. The asymptote begins at (0,0) where Quadrant 1 is.

BQ#3 – Unit T Concepts 1-3

• How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Tangent?

Tangent is equal to sin/cos. It is undefined when cos=0. When sin=0, tangent goes through the x-axis since tan=0.

Cotangent?

Cotangent is equalled to cos/sin. In Quadrant 1, t will be positive since the sin and cos graphs are positive. If the sin=1, cotangent will have asymptotes. In Quadrant 2, cos is negative; sin is positive. In quadrant 3, cos is negative; sin is negative. Their signs cancel out to make a positive cotangent. In Quadrant 4, cos is positive; sin is negative. This will give cotangent a negative answer.

Secant?

The reciprocal of secant is 1/cos. If cos=0, sec is undefined and will not touch. However, if the cos=1, sec amplitudes will touch.

Cosecant?

The reciprocal of cosecant is 1/sin. If sin=0, cosecant is undefined and will not touch. However, if sin=1, csc amplitudes will touch.

BQ#5 – Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

The Unit Circle has ratios for trig functions. Sin=y/r, cos=x/r, tan=y/x, csc=r/y, sec=r/x, and cot=x/y. The asymptote is only present when the denominator is equal to 0. However, since r is always equal to 1 in the Unit Circle triangles, this will give us an actual number value for sine and cosine. For us to have an asymptote, we would have to have an undefined answer like in the other four trig graphs give us.

BQ#2 – Unit T Concept Intro

How do the trig graphs relate to the Unit Circle?
ANSWER: Trig graphs relate to the Unit Circle because we just have to imagine the Unit Circle being "unwrapped" into a straight line. This would be like the x-axis of the trig graphs. We have to imagine the Unit Circle still having its coordinates.

• Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

ANSWER: The period of sine and cosine is 2pi because of their positives and negatives. From quadrant one through four, sine is positive, positive, negative, negative. We imagine sine on the unit circle in portions. At 0* it is 0. At 90* it is 1. At 180* it is 0. At 270* it is -1. At 360* it is 0. These are literally the points on the graph that give sine a mountain-to-valley image. For cosine it is reflected, so we start with a valley then turn into a mountain. For tangent and cotangent, the signs from quadrant one to four are positive, negative, positive, negative. Within this "unwrapped unit circle" we only see two periods. However, this kind of graph only shows us half of the period, hence, it is pi.

• Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

ANSWER: Sine and cosine have amplitudes of one because the Unit Circle's coordinates are at (0,1), (0,-1), (1,0), and (-1,0). If you look at (0,-1) and (0,1), these points are the graph's highest and lowest points on the graph. The amplitude is not going to pass one because that is where it reaches it's highest point, and it is at its lowest point at -1.

BQ# 1: Unit P

2. Law of Sines
SSA is ambiguous because we don't know if we will have no triangles, one triangle, or two triangles. We are only given one angle in this case. Now thinking back to the Unit Circle, we should remember how the lines on the circle are given to us by using Law of Sines when the radius is not equal to 1 as it has been given to us in Unit N.

4. Area Formula
The base is b and h is the height of the triangle. Here are are not given the height, so we have to use arcsin of the angle which, in this case, is equal to h/a. We are using opposite over hypotenuse for whatever angle we are using; in this case, it is angle C. We then take sin of the angle times 1/2ab. However, sometimes it won't have a and b given, so we have to take what is given and make sure we haves its opposite angle. All the sides must be different, so just think of all the variables in the equation being different. Here are the other formulas we can use:
A= 1/2bcsinA
A=1/2acsinB
A=absinC

http://www.compuhigh.com/demo/lesson07_files/oblique.gif

Works Cited
http://www.compuhigh.com/demo/lesson07_files/oblique.gif

I/D3: Unit Q - Pythagorean Identities

Inquiry Activity Summary

The Pythagorean is here again. We first saw it in unit N in the unit circle, and it relates to trig identities as well. Using x, y, and r, we can show that. (x^2/r^2)+(y^2/r^2)=(r^2/r^2) which is also (x^2/r^2)+(y^2/r^2)=1. This can be simplified to (x/r)^2+(y/r)^2=1. sin2x+cos2x=1 comes from the unit circle. The ratio for cosine on the unit circle is x/r. The ratio for since is y/r. Here we are going to take one of the magic 3 ordered pairs: 30 degrees. cos30 is equal to radical 3 over 2 and sin30 is equal to 1/2. Radical 3 over 2 squared is equal to 3/4. 1/2 squared is equal to 1/4. 3/4+1/4=1 which is where you get the one on the right side. Since we squared these fractions, we have to show it in our identities also. This identity is actually the Pythagorean theorem moved around, hence it is also called the Pythagorean identity. Keep in mind that an identity is "a proven fact and formula that is always true." This tactic works with any degree from the magic 3.

We can also derive the secant and tangent from sin2x+cos2x=1. If you divide all of that by cos2x, you will end up with tan2x+1=sec2x. With tanx=sinx/cosx, multiply the left and right sides by themselves to get a squared value for both. tanx*tanx=(sinx/cosx)(sinx/cos). In the end you will get tan2x=sin2x/cos2x.

Inquiry Activity Reflection

1. The connections that I see between Units N, O, P, and Q so far are that they all relate to triangle and they all use the six trig functions.
2. If I had to describe trigonometry in THREE words, they would be challenging, connected, and unexceptional.

WPP#13-14: Unit P Concept 6 & 7 - Law of Sines/Cosines

This WPP 13-14 was made in collaboration with Tracey Pham. Please visit the other awesome posts on her blog by going HERE.

WPP #12 Unit O Concept 10: Angle of Depression and Elevation

Elevation
Yoshi is filming his music video and wants to have his shot at the beach. For one of his shots, he is going to be standing at the top of a lighthouse while the camera will be on the floor 18 feet away from the lighthouse. The angle of elevation from the camera lense to the top of the lighthouse is 34*14'. What is the height of the lighthouse?

Answer: 12.25 m

Elevation

Depression

Yoshi is now on the other side of the lighthouse. He hears his fans cheering him on from below 36.8 m away and looks straight at them and waves. What is the angle of depression if he was standing on the same leveled lighthouse? (Hint: disregard the orange-ish lines labeling 12.25 m; the lighthouse from Yoshi to the floor is 12.25)

Answer: 34.24*

Depression


SHOW YOUR WORK

I/D2: Unit O - Derive the SRTs

INQUIRY ACTIVITY SUMMARY
As seen in the square, you have to cut it diagonally because that is how you can get two triangles. If they are equally bisected, they will form two 45-45-90 triangles. You get the hypotenuse by using the Pythagorean theorem (a^2+b^2=c^2). We are told that the side lengths of the square are 1. That means the side lengths of a and b of the triangle are 1 as well. You take (1)^2+(1)^2=c^2. That will give you c=radical 2; this is your hypotenuse. "n" means the variable used to find your sides. Since in a 45-45-90 degree triangle the sides corresponding to the 45 degree angles are the same, we can label them with "n." 





In the 30-60-90 triangle, I got it by bisecting an equilateral triangle down the center. Since the sides of the equilateral are equal to 1, I knew the hypotenuse was 1. The base is 1/2 since we cut the triangle in half. I then used Pythagorean theorem to find the height which gave me a=radical 3 over 2. This translates to the normal pattern because side a is n equal to n. The hypotenuse is double that. Here we see that side a (1/2) was multiplied by 2. (2)(1/2)=1; that is our hypotenuse. To find the height, we are most familiar with n radical 3. Our n in 1/2. We multiply that by radical 3. That gives us radical 3 over 2 as our height. We use n because that's the variable we are most familiar with when we first learned about triangles in geometry. In this problem the b is n, the hypotenuse is 2n and the height is n radical 3.

INQUIRY ACTIVITY REFLECTION

Something I never noticed before about special right triangles is
that they can be made from squares and triangles. After learning the unit circle, I thought special triangles were only used in that.
Being able to derive these patterns myself aids in my learning because
I now better understand my last unit as well as understand where my values come from. Before I just had to memorize the values of each side without knowing how I got them.

I/D1: Unit N - How do SRT and UC relate?

INQUIRY ACTIVITY SUMMARY
Describe the 30* triangle
Click HERE.
Describe the 45* triangle
Click HERE.
Describe the 60* triangle
Click HERE.


1. The coolest thing I learned from this activity was...
how to find these points and coordinates mathematically instead of memorizing it by heart.
2. This activity will help me in this unit because...
I can now better understand how to label my triangles and my unit circle. It also showed me patterns I didn't notice before.
3. Something I never realized before about special right triangles and the unit circle is…
that they actually relate to each other! I was told that in past math courses, but I didn't quite grasp what it meant.

RWA#1: Unit M Concept 5: Graphing Ellipses Given an Equation and Identifying All Parts

1. The mathematical definition of an ellipse is "the set of all points such that the sum of the distance from two points is a constant." (http://www.mhhe.com/math/precalc/barnettca2/student/olc/graphics/barnett01caaga_s/ch07/downloads/pc/ch07section2.pdf)

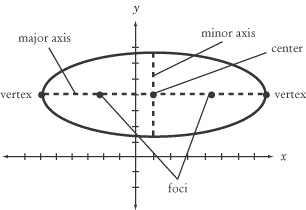
2. An ellipse is algebraically shown with the equation written in standard form: (x-h)^2/a^2+(y-k)^2/b^2=1 or (x-h)^2/b^2+(y-k)^2/a^2.  The center is always (h,k).  "a" is always bigger than "b."  Remember that a and b are squared in the equation, so you have to take the square root of them when writing them out on the template.

It can be graphically shown as a visual on a graph.  An ellipse typically looks like a squished circle from its sides or top and bottom.

Here is how you can identify key parts on the graph:
If a is under x in the equation (the first one listed above), the graph will be fat. The major axis length is 2a (Mrs. Kirch shows this with a solid line); the minor axis length is 2b (she shows this with a dotted line). In this kind of equation, the major axis will run horizontally.
To find vertices: Count "a" units from the center going left and right; plot these points. To find co-vertices: Count "b" units from the center going up and down; plot these points.

If a is under y in the equation (the second one listed above), the graph will be skinny. The major axis length is 2a; the minor axis length is 2b.  In this kind of equation, the major axis will run vertically.  To find vertices: Count "a" units from the center going up and down; plot these points. To find co-vertices: Count "b" units from the center going left and right; plot these points.

The foci effects the shape because the further away it is to the vertices, the more it will have to "focus" on that point.  When the foci increases, the eccentricity does, too. To find your foci, the major axis value will be the number that does NOT change in the foci points. (ex. If the major axis is y=-2, your two foci will be (#, -2).) To find the other number, (ex. It would be x.), you take the value from your minor axis and add AND subtract it to/from your c value.  In order to find c, you use the equation a^2+b^2=c^2.
Your eccentricity is greater than 0 but less than 1 and can be found with "c/a.

Do you want to see a problem worked out? Watch this video example.

3. A real world application of an ellipse would be when you tilt your glass cup with a drink to take a sip out of it. The drink in your cup will form an ellipse around the cup's interior.  Let's take for example a glass of milk.  When the milk is in the cup and set on the table, you may notice the top of the milk is shaped as a circle. Once you begin to tilt the cup and bring it to your mouth for a sip, the shape at the top of the milk is no longer a circle.

The ellipse is formed because the eccentricity has increased. It will continue to increase as you tilt the cup. The center of the ellipse moves further from the center of the cup the more you title your cup.  I would associate this example as a skinny ellipse represented with the equation (x-h)^2/b^2+(y-k)^2/a^2 because the cup's ellipse would be facing me. The point closest to my lip and furthest to me would be the vertices.  The left and right side of the cup would be my co-vertices.

4. Works Cited
Ellipse Image pasted from: http://img.sparknotes.com/content/testprep/bookimgs/sat2/math2c/0006/ellipse.gif
Tilted Milk Cup Image pasted from: http://lisamasson.photoshelter.com/image/I0000RM3hrmrL0Po
Ellipse Video Example video from: http://www.youtube.com/watch?v=wTGA9D4Y0qk

Ellipse website link pasted from: http://www.mhhe.com/math/precalc/barnettca2/student/olc/graphics/barnett01caaga_s/ch07/downloads/pc/ch07section2.pdf